尺寸的多维度探究从物理到哲学的视角

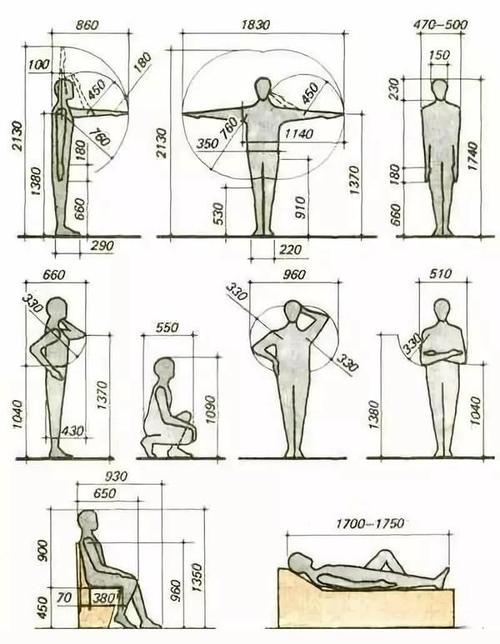
尺寸，作为描述物体大小和空间关系的概念，贯穿于自然科学、工程技术乃至哲学思考的多个领域。本文旨在从物理学、数学和哲学的角度，探讨尺寸的本质、测量方法及其在不同学科中的应用和意义。

物理学中的尺寸

1. 尺寸的定义与测量

尺寸的物理意义：长度、宽度、高度和体积的量化。

测量技术：直尺、卡尺、激光测距等工具的应用。

误差分析：测量过程中的不确定性和误差来源。

2. 尺寸在物理定律中的作用

牛顿力学：物体尺寸对运动和力的影响。

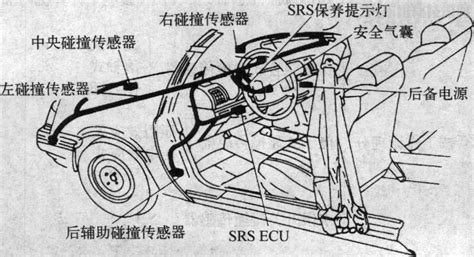
量子力学：尺寸与粒子行为的关联，如波粒二象性。

相对论：尺寸在高速和强引力场中的变化。

数学中的尺寸

1. 几何学中的尺寸

点、线、面、体的尺寸特征。

多维空间：超越三维的几何结构。

2. 拓扑学与尺寸

拓扑不变量：尺寸在拓扑变换中的保持性。

分形几何：自相似性和非整数维度。

哲学中的尺寸

1. 尺寸的认知意义

人类对尺寸的感知与认知局限。

尺寸概念在不同文化中的差异。

2. 尺寸的形而上学探讨

尺寸与存在的关系：物体存在的必要条件。

尺寸与无限：宇宙的边界与无限小的粒子。

结论

尺寸作为一个基础而复杂的概念，不仅在科学研究中扮演着关键角色，也激发了哲学上的深刻思考。通过跨学科的视角，我们能更全面地理解尺寸的多重意义和其在人类知识体系中的位置。

参考文献

1. Feynman, R. P., Leighton, R. B., & Sands, M. (1963). The Feynman Lectures on Physics, Vol. I. AddisonWesley.

2. Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. W. H. Freeman and Company.

3. Weyl, H. (1952). Symmetry. Princeton University Press.

4. Penrose, R. (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Alfred A. Knopf.

本文通过对尺寸在物理学、数学和哲学中的探讨，展示了这一概念的丰富内涵和广泛应用，为读者提供了深入理解尺寸的多维度视角。